|
Computing the Distance Between Two Stars or Planets
In this case of computing the distance between two stars or planets, we are treating the bodies as simple points in 3D space. So, finding the distance between them, becomes a simple matter of 3D trigonometry.
In astronomy, we generally give stars 3D spherical coordinates. They are the standard right ascension, declination and distance coordinates of the stars. On Earth we use longitude and latitude, in astronomy, we use right ascension and declination respectively as coordinates. These standard space coordinates are cataloged for many stars (Epoch J2000 is used here) and they can be used for 3D computations to the extent of their accuracy.
The 3rd coordinate, the distance, is often symbolized by R because it represents the radius vector (radius of a sphere), the line directed between the eye and body. The coordinates are envisioned as a grid drawn on the surface of an infinitely large sphere with our eye at the center and the body at distance R from the eye with apparent longitude (right ascension) and latitude (declination) coordinates as viewed projected against the sphere.
From the spherical space coordinates (α, δ, R), we can compute the corresponding rectangular (X, Y, Z)
coordinates from which the linear spatial distance (D) between the two bodies can then be computed.
For any given star/planet, let:

Given the spherical ( α, δ, R) coordinates of a planet or star, its corresponding
rectangular ( X, Y, Z) coordinates may be computed from:
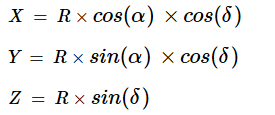
Given the spherical ( α, δ, R) coordinates for two bodies, distinguished by subscripts, to compute the distance between the bodies, we first compute their corresponding rectangular ( X, Y, Z) coordinates:
For the first body:
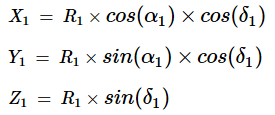
For the second body:
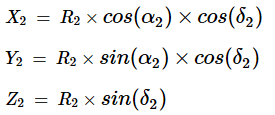
The distance (D) between the two bodies in XYZ-space may then be computed as the
square root of the sum of the squares of the differences between their rectangular
coordinates:
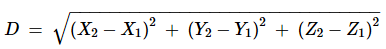
A Numerical Example - Part 1:
In this example we will compute the distance between the bright stars Sirius (= 1st Body) and Vega (= 2nd Body) and then compute how bright each star would appear to be from the perspective of the other.
This is the computational data pertaining to the stars used in the example:
J2000.0 CATALOG DATA FOR SIRIUS AND VEGA AS VIEWED FROM EARTH/SUN
ASSUMED DISTANCE UNITS = LIGHT YEARS
-------- --------------- ---------------- ------- -------
1ST STAR RIGHT ASCENSION DECLINATION DIST VIS MAG
Sirius 06h 45m 08.9s -16° 42' 58" 8.6 -1.46
101.2870833 deg -16.7161111 deg
-------- --------------- ---------------- ------- -------
2ND STAR RIGHT ASCENSION DECLINATION DIST VIS MAG
Vega 18h 36m 56.3s +38° 47' 01" 25.3 +0.03
279.2345833 deg +38.7836111 deg
Performing the distance computations for the given data (angles expressed in degrees):
DISTANCE BETWEEN THE STARS SIRIUS AND VEGA
Rectangular Coordinates of Sirius:
x1 = 8.6 * Cos(101.2870833) * Cos(-16.7161111) = -1.6121048578
y1 = 8.6 * Sin(101.2870833) * Cos(-16.7161111) = 8.0772729746
z1 = 8.6 * Sin(-16.7161111) = -2.4736166278
Rectangular Coordinates of Vega:
x2 = 25.3 * Cos(279.2345833) * Cos(+38.7836111) = +3.1648925282
y2 = 25.3 * Sin(279.2345833) * Cos(+38.7836111) = -19.4661817544
z2 = 25.3 * Sin(+38.7836111) = +15.8474358553
Rectangular Coordinate Differences:
dx = (x2 - x1) = +4.7769973860
dy = (y2 - y1) = -27.5434547290
dz = (z2 - z1) = +18.3210524831
The distance (D) between the stars Sirius and Vega may
then be found from:
D = SqRoot(dx*dx + dy*dy + dz*dz) = 33.4233835290
= About 33.42 light years between the stars.
APPARENT BRIGHTNESS
Once we know the distance ( D) between two bodies, we may then determine how bright each body would appear to be (ideally) as viewed from the other's perspective, as opposed to their apparent magnitudes as viewed from Earth.
In this case, the general stellar magnitude vs. distance
formula may be expressed as:
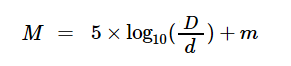
Where:
m = Visual magnitude of body as viewed from distance d in any units
M = Visual magnitude of body as viewed from distance D in any units
and m respectively refer to the distance to and visual magnitude of one of the bodies as viewed from Earth.
D is the distance between the two bodies previously computed above.
M is the visual magnitude of one of the bodies at distance D.
The known values are ( d, m, D) from which we compute M for each body.
Numerical Example Continued - Part 2:
From Sirius (Body 2) as viewed from Vega (Body 1):
m = +0.03 = Magnitude of Vega as viewed from Earth
d = 25.3 = Distance to Vega from Earth in light years
D = 33.423 = Distance between Sirius and Vega in light years
M = Magnitude of Vega as viewed from Sirius
M = 5*Log10(D/d) + m
M = 5*Log10(33.423/25.3) + 0.03
= 0.604625 + 0.03 = 0.634625
So, from Sirius, the magnitude of Vega would be +0.63
==============================================================
From Vega (Body 1) as viewed from Sirius (Body 2):
m = -1.46 = Magnitude of Sirius as viewed from Earth
d = 8.6 = Distance to Sirius from Earth in light years
D = 33.423 = Distance between Sirius and Vega in light years
M = Magnitude of Sirius as viewed from Vega
M = 5*Log10(D/d) + m
M = 5*Log10(33.423/8.6) + (-1.46)
= 2.947735 - 1.46 = 1.487735
So, from Vega, the magnitude of Sirius would be +1.49
Jay Tanner - 2025
|