There are times when we may want to know how bright the sun would appear to be if viewed from a different perspective, such as how bright our sun might appear to be if viewed from Mercury or Pluto or even from another star many light years away.
This program applies the following magnitude versus distance formula to the problem of computing the apparent ideal visual stellar magnitude of the sun as viewed from any given distance expressed in astronomical units, light years or parsecs.
NOTE:
Space is being treated as 'crystal-clear' and free of any obscuring gas or dust, which is adequate for our purposes here.
Visual Magnitude vs. Distance
The general magnitude vs. distance formula may be expressed as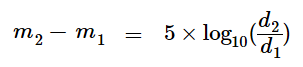
Eq. 1
Where:
m1 = Visual magnitude of a body as viewed from distance d1
and
m2 = Visual magnitude of the same body as viewed from distance d2
In this case, the astronomical body is the Sun, but it could be a star, the moon, a planet, an asteroid, etc. Given any three known values, using Equation 1 above, we can directly derive the remaining unknown value.
When dealing with the basic problem of apparent stellar brightness and magnitude variation versus distance, there are three general units of distance we might apply, depending upon which is most convenient for the kind of work being done. These units are astronomical units (AU), light years (LY) and parsecs (pc).
Generally, we can say that for any distance units defined in terms of AUs:
The following three visual magnitude versus distance equations were formulated specifically for application to the sun and were derived from Equation 1 and the computational data given above.
For solar distance reckoned in astronomical units (AU):
For solar distance reckoned in light years (LY):
For solar distance reckoned in parsecs (pc):
This program applies the following magnitude versus distance formula to the problem of computing the apparent ideal visual stellar magnitude of the sun as viewed from any given distance expressed in astronomical units, light years or parsecs.
NOTE:
Space is being treated as 'crystal-clear' and free of any obscuring gas or dust, which is adequate for our purposes here.
Visual Magnitude vs. Distance
The general magnitude vs. distance formula may be expressed as
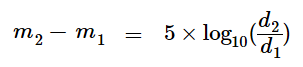
Eq. 1
m1 = Visual magnitude of a body as viewed from distance d1
and
m2 = Visual magnitude of the same body as viewed from distance d2
In this case, the astronomical body is the Sun, but it could be a star, the moon, a planet, an asteroid, etc. Given any three known values, using Equation 1 above, we can directly derive the remaining unknown value.
When dealing with the basic problem of apparent stellar brightness and magnitude variation versus distance, there are three general units of distance we might apply, depending upon which is most convenient for the kind of work being done. These units are astronomical units (AU), light years (LY) and parsecs (pc).
WORKSHEET A
We first need to define some constants and derived working values.
The extra precision is for internal computational purposes. The
final computed result can be rounded to whatever precision is
practical.
-26.74 = Visual magnitude of the sun at 1.0 AU (NASA)
1 AU = 149597870700 m (NASA/IAU/2012)
Light Speed = 299792458 m/s (NIST)
1 Standard (Julian) Year = 365.25 days = 31557600 seconds
For light years and parsecs, we derive the following:
1 LY = (Light Speed) * (Seconds per Standard Year)
= (299792458 m/s) * (31557600 s)
= 9460730472580800 m
From which we derive the number of AUs per light year:
AU_PER_LY = (9460730472580800 m/LY) / (149597870700 m/AU)
= 63241.0770842662802686 AU/LY
Since 1 parsec is the distance at which the sun has a parallax shift
of 1 second of arc, a parsec, expressed in AUs, equates to the number
of seconds of arc in a unit radian or 206264.806247 AUs per parsec.
ARCSEC_PER_RADIAN = ARCSEC_PER_DEG * 180 / pi
= 3600 * 180 / 3.1415926535897932
= 206264.8062470963551565 arcsec/rad
AU_PER_PC = ARCSEC_PER_RADIAN
= 206264.8062470963551565 AU/pc
Generally, we can say that for any distance units defined in terms of AUs:
WORKSHEET B Generally: m = 5 * log10(AU_PER_DISTANCE_UNIT) - 26.74 For visual magnitude of the sun at 1.0 AU: m = 5 * log10(AU_PER_AU) - 26.74 = 5 * log10(1) - 26.74 = 5 * 0 - 26.74 = -26.74 For visual magnitude of the sun at 1.0 LY: m = 5 * log10(AU_PER_LY) - 26.74 = 5 * log10(63241.077084) - 26.74 = 5 * 4.800999 - 26.74 = -2.735 For visual magnitude of the sun at 1.0 pc: m = 5 * log10(AU_PER_PC) - 26.74 = 5 * log10(206264.806247) - 26.74 = 5 * 5.314425 - 26.74 = -0.1679 So, we have now derived the constants for the three distance units and can derive equations specific to each unit of measure: -26.74 = Visual magnitude of sun at distance of 1.0 AU -2.735 = Visual magnitude of sun at distance of 1.0 light year -0.1679 = Visual magnitude of sun at distance of 1.0 parsec
The following three visual magnitude versus distance equations were formulated specifically for application to the sun and were derived from Equation 1 and the computational data given above.
For solar distance reckoned in astronomical units (AU):
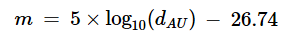
Eq. 2
For solar distance reckoned in light years (LY):
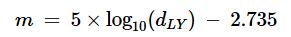
Eq. 3
For solar distance reckoned in parsecs (pc):
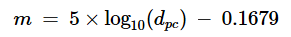
Eq. 4
Ref:
Solar visual magnitude at
http://nssdc.gsfc.nasa.gov/planetary/factsheet/sunfact.html
Speed of light (
http://physics.nist.gov/cgi-bin/cuu/Value?c|search_for=light
Solar visual magnitude at
1.0 AU (-26.74) came from the NASA solar factsheet:http://nssdc.gsfc.nasa.gov/planetary/factsheet/sunfact.html
Speed of light (
299792458 m/s) came from NIST:http://physics.nist.gov/cgi-bin/cuu/Value?c|search_for=light
Jay Tanner - 2025 - v3.0